 This circuit is based on a passive infrared (PIR) sensor, which automatically switches on a device when someone comes close to it. It can be used for detection of theft or an unauthorised person entering a restricted area or building. It can also turn on lights when someone approaches the area where it is installed. Applications of this circuit include security systems, corridor lights and bathroom lights, among others.
This circuit is based on a passive infrared (PIR) sensor, which automatically switches on a device when someone comes close to it. It can be used for detection of theft or an unauthorised person entering a restricted area or building. It can also turn on lights when someone approaches the area where it is installed. Applications of this circuit include security systems, corridor lights and bathroom lights, among others.
Circuit and working
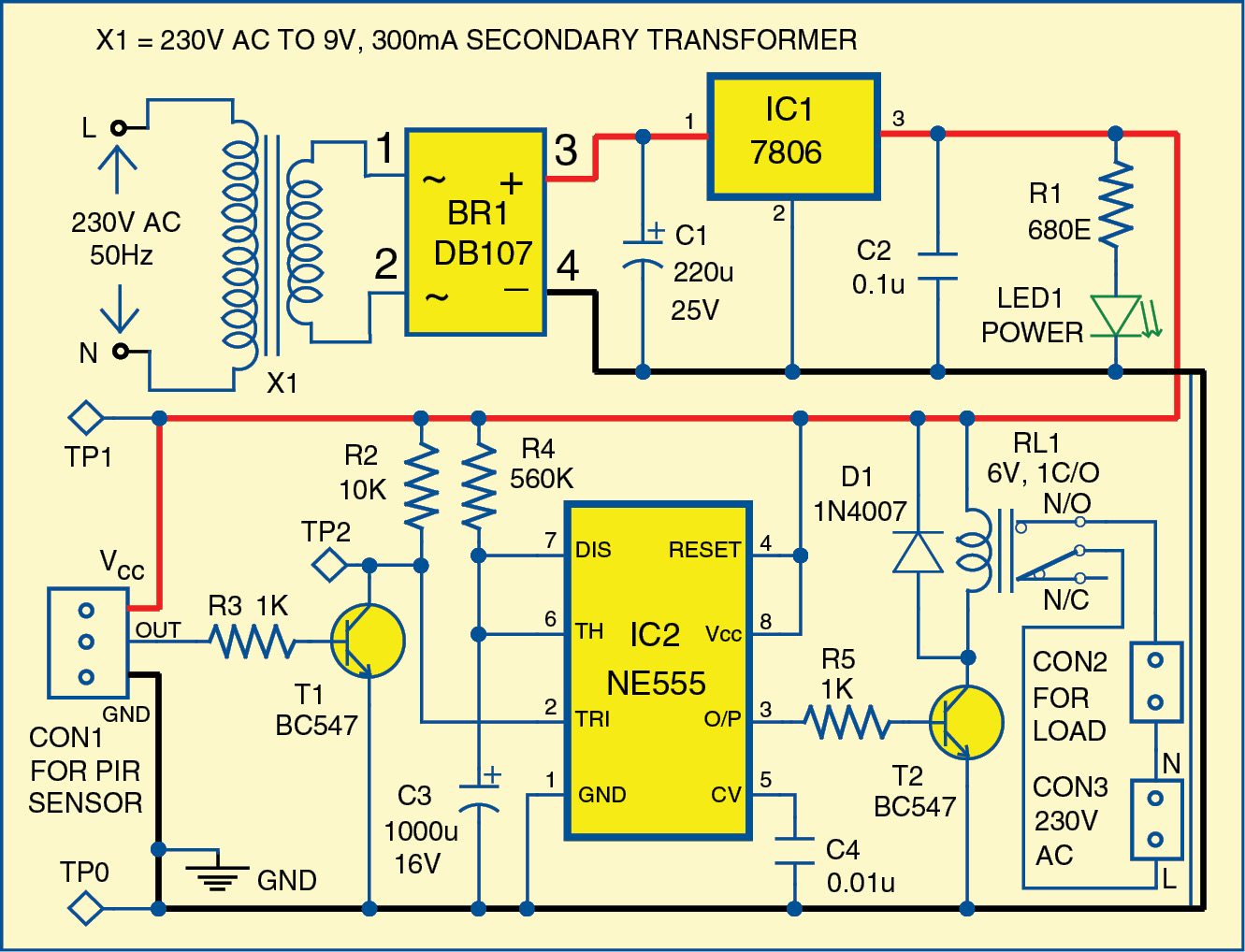
 The circuit diagram of the motion detector using NE555 timer is shown in Fig. 1. It is built around 230V AC primary to 9V, 300mA secondary transformer X1, bridge rectifier DB107 (BR1), 6V voltage regulator 7806 (IC1), timer NE555 (IC2) and a few other components.
The circuit diagram of the motion detector using NE555 timer is shown in Fig. 1. It is built around 230V AC primary to 9V, 300mA secondary transformer X1, bridge rectifier DB107 (BR1), 6V voltage regulator 7806 (IC1), timer NE555 (IC2) and a few other components.
The 230V AC mains is stepped down to 9V, 300mA through step-down transformer X1. Secondary output of X1 goes to bridge rectifier BR1. Capacitor C1 filters the ripples and the rectified output is given to regulator 7806 (IC1). IC1 provides 6V regulated DC output to operate the circuit. LED1 is used as a power-on indicator.
 IC2 is configured in monostable mode. Time period of IC2 is based on resistor R4 and capacitor C3, which is around ten minutes in this case. By changing resistor R4 and capacitor C3 you can change the time period of IC2.
IC2 is configured in monostable mode. Time period of IC2 is based on resistor R4 and capacitor C3, which is around ten minutes in this case. By changing resistor R4 and capacitor C3 you can change the time period of IC2.
Output pin 3 of IC2 is connected to the base of relay driver transistor T2. Contacts of relay RL1 are connected to the load, which could be a CFL or a bulb connected across CON2.
The PIR sensor is a pyroelectric device developed for detection of human body infrared radiations. It has a single output that goes high when a valid motion is detected. That is, the load is switched on whenever the PIR module senses a body in motion nearby.










cant we operate it on 5v dc power supply like mobile charger, it would have been easy.
yes gowhar.. you can do it, but this project include 6v dc relay, so it can’t be operate,
Better to use capacitor power supply for such Application.
can we use pir sensor without arduno
Yes, you can use PIR sensor without Arduino or microcontroller
sensitivity control?
Kindly elaborate your query.
Is the circuit working??
I tried it by replacing the load by a buzzer but it keeps ringing. Please help thank you ? ?
kindly check the register. you may also use variable register
How to reset timer when second motion detected???
ITS Not working, IC and voltage regulator are over heated.When initially power on relay is activated and not sensing the circuit
is this is a microcontroller basaed project
Sir please help
It’s not working .When initially power ON the relay is activated and not sensing .I remove the sensor but relay not OFF
The circuit not reset
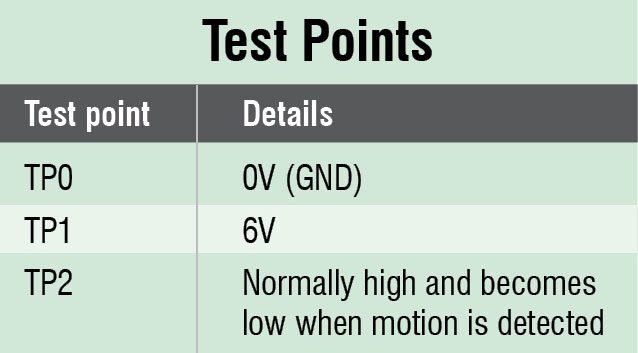
The relay should not get energised without PIR sensor input. First check proper connections in the circuit including correct polarities and orientations of various active components. If connections are ok, make sure that voltage at pin 2 of NE555 is high when sensor is not connected and low when sensor is connected and motion is detected.
Note that when power is switched on, the relay will energise for around ten minutes. If relay is not de-engerise even after ten minutes, first check whether transistor BC547 is faulty or connected in wrong position. If it is ok, next check IC2.
The relay should not get energised without PIR sensor input. First check proper connections in the circuit including correct polarities and orientations of various active components. If connections are ok, make sure that voltage at pin 2 of NE555 is high when sensor is not connected and low when sensor is connected.
instead of transformer ,,, how to supply 9v to this device
sir
i want to make a muscal buzer with the use of bt66 transister and 27mm 3-pin piezo,
i have been try many time but i’m not 100% succes.
so please help me
What is the range of PIR mean from how much area can be covered.
how can i connect the transformer to the circuit? please help. im currently making this project
try solder
Why you did’t use a transistor to switch relay instead of using 555 ic. As there are no time events, this circuit can be made by only switching the transistor when pir sensor pin give output.
if you didn’t use the 555 ic there will be no timer to stop the load after 10 minutes