1 Preface
In the data sheet for Siglent’s SDG2000X arbitrary waveform generator series, the sampling rate specification (1.2GSa/s) is followed by a note of “4X Interpolation”.
| Sampling Rate | 1.2 GSa/s (4X Interpolation) |
| Vertical Resolution | 16 bit |
This be confusing to some customers, even some experienced users of function generators. This white paper is intended to explain this specification and to discuss the advantages of the Interpolated DDS technique compared to a traditional DDS based function generator.
2 Profile of Traditional DDS
The figure below shows the basic design of the traditional DDS technique,in which digital waveform data is output in response toa reference clock for the DDS circuitry, then converted by the D/A converter using the same clock. That is to say, in a traditional DDSstructure the clock for the DDS and for the D/A converter run at the same frequency.
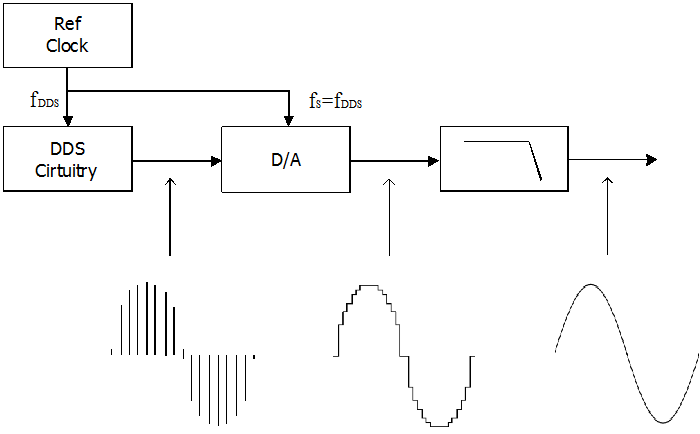
A reconstruction filter following the D/A converter helps to smooth the steps from the D/A’s output in order to produce a smoother, more “analog” signal.
3 Introduction to Interpolated DDS
The figure below shows the structure of the Interpolated DDS. An interpolator is inserted between the DDS circuitry and D/A converter. In this structure, digital waveform data is output in response to the reference clock of the DDS circuitry, interpolated by “I” (in SDG2000X I = 4), and then converted by the D/A, with a sampling clock“I” times the frequency of the reference clock.After the D/A convertor, a reconstruction filter is also applied.
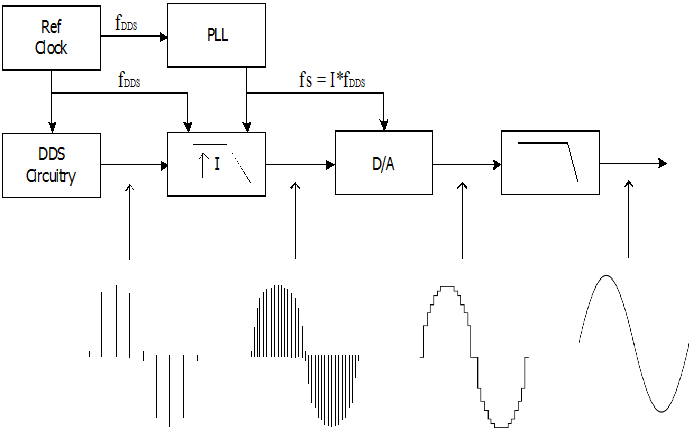
Siglent’sSDG2000X applies this technique with the interpolation factor I = 4. The reference clock of the DDS circuitry on the SDG2000X is 300MHz.Using the interpolation circuitry, the sampling clock of the D/A convertor is increased to 1.2GHz. This is the explanation behind 1.2 GSa/s specification found in the data sheet – 1.2GSa/s followed by a “4X interpolation” note.
This explains the mechanics behind the interpolated sampling technique.However, what is the technical reasoning behind Siglent’s innovative sampling technique?
4 Why Interpolation?
4.1 To Break the Bandwidth Limit
First, let’s compare the waveform in the time domain using the two different sample rates.
Looking at the output waveform of the D/A, the 1.2GSa/s sample rate results in smaller steps (higher resolution) than with the 300MSa/s sampling clock (Fig 3).
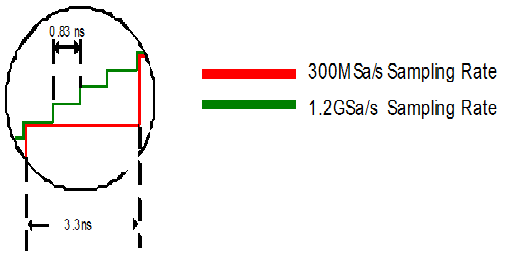
The reader may ask, “If both waveforms are to be passed through a restructuring filter in order to smooth the waveform steps, then the sample rate should not matter.” The fact is, the step size does affect the final smoothed waveform.
Now let’s look at this difference in the frequency domain in order to get a clearer understanding.
The figure below shows a spectrum example in which an 80MHz sine wave is output by a D/A with 300MSa/s. Output spectrum of the D/A includes the fundamental, and its image frequencies.
Amplitudes of all the spectrum components comply with the sin(x)/x envelope. Usage of the reconstruction filter is to filter all of the image frequencies which are located outside the Nyquist bandwidth.
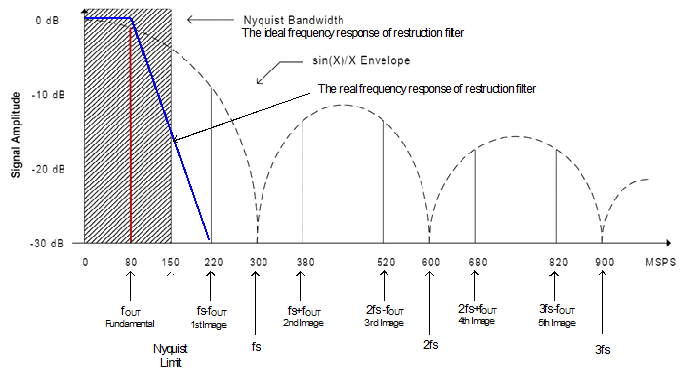
An ideal reconstruction filter should retain all the signals located in the Nyquist bandwidth, and filter out the ones outside it. In other words, its frequency response should be coincident with the Nyquist bandwidth, as the shadow part in Figure 4.In this case, the maximum frequency can reach the Nyquist Limit (e.g. 1/2 sampling clock frequency).
As we know, in engineering the ideal filter with “brick wall” response doesn’t exist. In the real world, filters actually have some degree of roll off.
Figure 4 shows the spectrum of the output from a 300 MSa/s A/D converter with an output frequency of 80 MHz. The nearest image occurs at 220 MHz so the maximum roll off would occur at 140 MHz.
But for a 150MHz signal, the nearest image is 300 – 150 = 150MHz, the space remaining for roll off is zero, which is not realizable. Generally, the limit bandwidth of a reconstruction filter is 40% of the sampling clock. That is to say, for a 300MSa/s D/A, the maximum available output frequency is 120MHz.
The figure below shows 2 reconstruction filter designs with roll offs from 120MHz to 180MHz.Both designs are 9-order elliptic filters.The difference is the design on the left uses ideal components, and the one on the right uses real-world components, with parasitic parameters. As we can see, a real filter has an extra ~3dB attenuation on the corner frequency (i.e. 120MHz), and its attenuation performance on the stop band cutoff frequency (i.e. 180MHz) degrades.
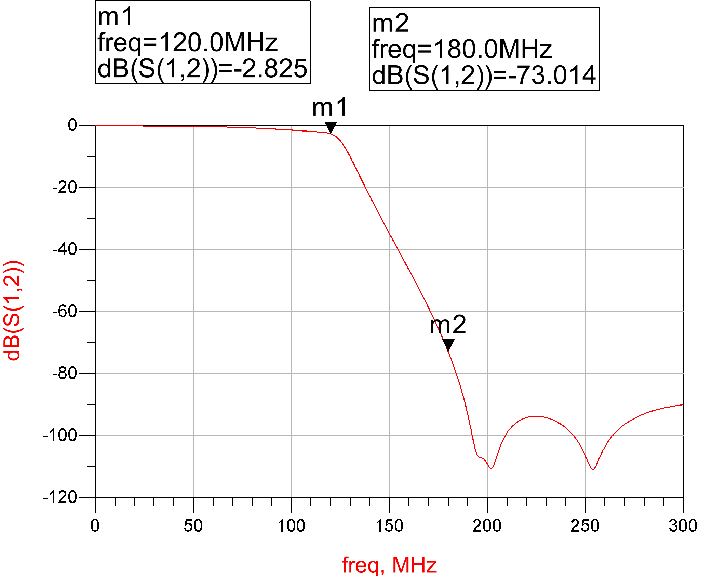
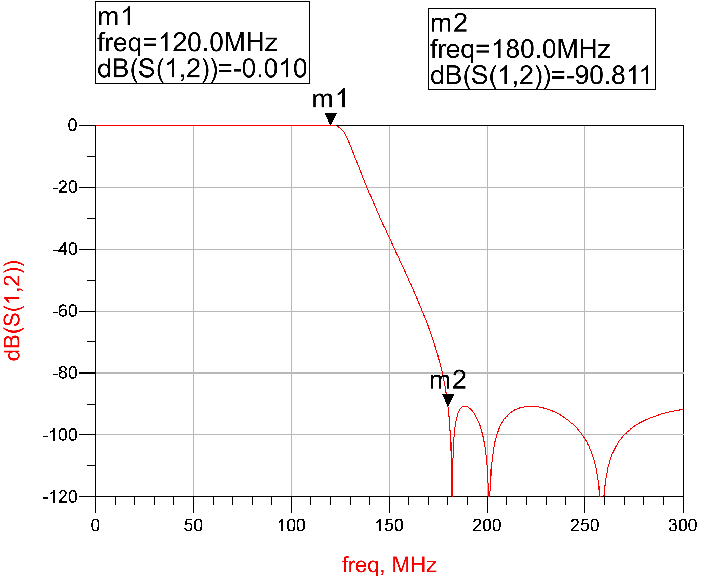
In addition, the sin(x)/x envelope of the D/A’s response itself will add attenuation to the signal. At 40% of the sampling clock (e.g. 120MHz in Figure 4), the attenuation caused by the D/A is about 2.4dB. An inverse sin(x)/x filter is generally necessary to compensate this attenuation.
If the sampling rate of D/A is 1.2GSa/s, for a 80MHz signal, the nearest image is 1.12GHz, so the maximum roll off of reconstruction filter could be 1.04GHz, as shown in Figure 6. Design of the reconstruction filter is greatly simplified.
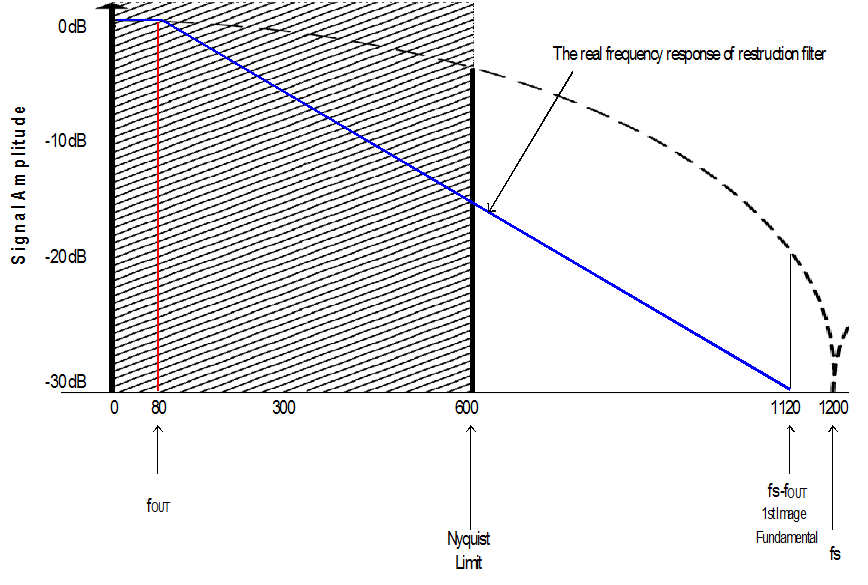
Figure 7 shows the real reconstruction filter design with roll off from 120MHz to 1.08GHz. This is much easier to achieve than the one with roll off from 120MHz to 180MHz.
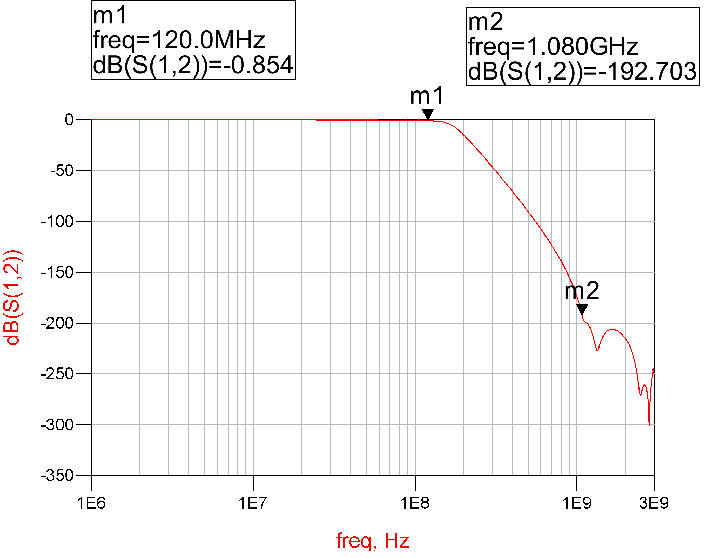
On the other hand, as the main lobe width of the sin(x)/x envelope increases, the attenuation contributed by the D/A decreases. At 120MHz, the attenuation caused by the 1.2GSa/s D/A is approximately0.14dB, which can be ignored in most cases. No more inverse sin(x)/x filtering is needed.
Based on the above, because of limits of the reconstruction filter a 300MSa/s D/A can only output a 120MHz maximum frequency. But a 1.2GSa/s D/A can achievea higher upper frequency limit.Of course in the interpolated DDS structure, the digital filter in the interpolator will restrict the frequency to the Nyquist limit of the DDS clock (e.g. 150MHz), but a digital filter is much easier to design than an analog reconstruction filter. Using the interpolated DDS,it is easy to raise the upper limit of output frequency from 120MHz to 130MHz or more.
4.2 To Remove the Spurs Generated by D/A Convertor
Intermodulation distortion isunavoidable in a D/A convertor. In a traditional DDS structure it is difficult to remove some inter-modulation distortion components between the clock and the output signal, such as 
The figure below shows an example with 120MHz output frequency and 300MSa/s sampling rate. The distortion fs – 2fout= 60MHz falls into the pass band of the reconstruction filter. It is not possible to be removed.
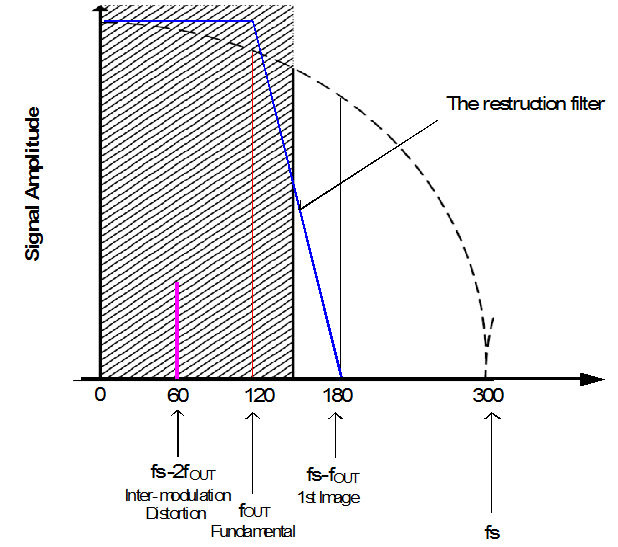
But with a 4X interpolated DDS structure, for 120MHz frequency output, the distortion components = 960MHz, =840MHz, which are located far away from pass band of the reconstruction filter.
5 Summary
Compared with a traditional DDS design, the Interpolated DDS technique inserts an interpolator between the DDS circuitry and the D/A convertor, yielding a higher sampling rate. With such a structure the design of the reconstruction filter is no longer the bottleneck for bandwidth. On the other hand, the problems due to intermodulation distortion products falling into the pass band of the reconstruction filter is solved, resulting in better SFDR performance.
6 Reference
[1] Analog Devices, A Technical Tutorialon Digital Signal Synthesis
[2] A.V. Oppenheim, R.W. Schafer, J.R. Buck, Discrete-time Signal Processing
