No storage media like CDs, DVDs, flash memories, solid-state devices/memories or telecommunication technologies like mobile communication, satellite communication, WiMAX, digital audio/video broadcasting (DVB), deep Space communication is perfect, and all of these experience some amount of errors. To prevent re-reading or re-transmission of information every time an error occurs, storage and communication systems are embedded with error correcting codes (ECC) technology.
History of coding theory

Pioneers of coding theory, Claude Elwood Shannon (1916-2001) and Richard Hamming (1915-1998), were colleagues at Bell Laboratories. Shannon’s channel coding theorem proves that if the information transmission rate is less than the channel capacity, it is possible to design an error correcting codes (ECC) with almost error-free information transmission. American mathematician Hamming pioneered this field and invented the first error correcting codes (ECC) in 1950. It is known as (7, 4) Hamming code.
There are various error-detection and correction techniques, which are suitable with specific noisy channels/media, like random error or burst error or multi-path distortion or channel effects. Error control coding approaches are forward error correction (FEC) and automatic repeat request (ARQ).
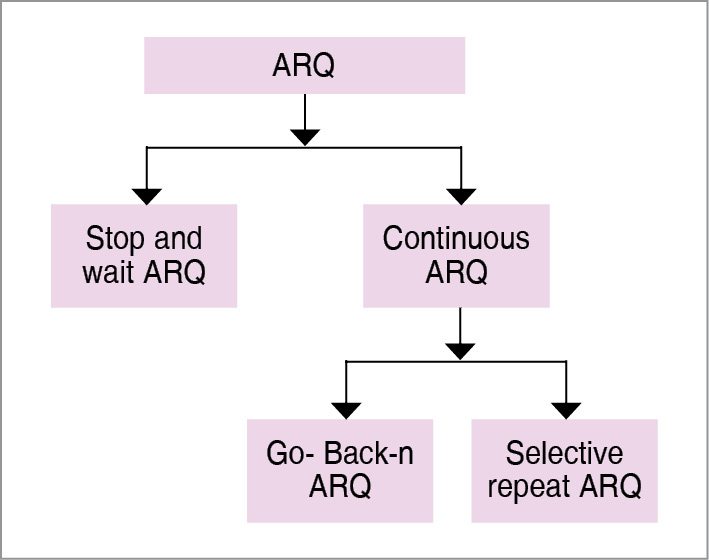
Error control for a one-way system is accomplished using FEC. For two-way communication, for example, telephone channel and some satellite communication systems, error correcting codes (ECC) are accomplished using error detection and retransmission called ARQ. Generalised classifications of ARQ and FEC are shown in Figs 2 and 3, respectively.
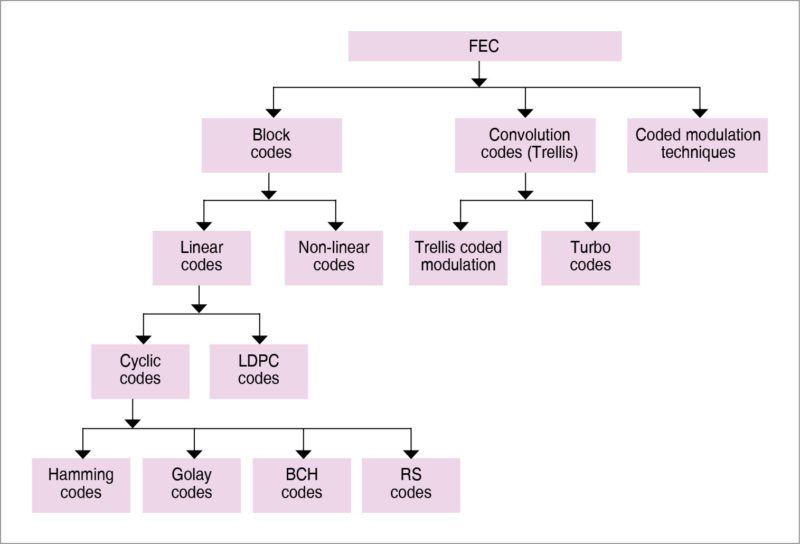
Taxonomy of FEC techniques
Block codes. In this coding scheme, each k-bit information block is converted to an n-bit coded block with (n-k) redundant bits added to k-bit symbols. These redundant bits are referred as parity bits that do not carry any information. The resulting code is referred to as (n, k) block code. Here, the code rate is defined as k/n.In binary block codes, 2k k-bit message sequences are uniquely mapped into 2k n-bit codes, out of possible 2n n-bit codes.
Convolutional codes. In this, a code-word depends not only on the corresponding k-bit message block at the same time, but also on m previous message blocks. Hence, the encoder has a memory order of m. Because the encoder contains memory, it is implemented with sequential logic circuits. Convolutional codes are widely accepted, and advancement or improvement to this coding scheme have resulted in two new coding schemes, namely, Trellis coded modulation (TCM) and turbo codes.

Coded modulation techniques. In both block and convolutional coding schemes, coding gain is achieved with the price paid for the bandwidth. Since in these schemes k-bit information signal is replaced by n-bit coded words (n>k), the required bandwidth gets increased, which is a major bottleneck for band-limited channels such as telephone channels.
To overcome this problem, combined modulation and coding schemes are considered. In this case, coding gain is achieved with the price paid for the decoder complexity. Different coded modulation techniques are Trellis coded modulation, block coded modulation, multi-level coded modulation and turbo coded modulation.
Application areas for error correcting codes (ECCs)
Deep Space communication. Without an error-correction scheme, Voyager and Galileo would not have been able to send the volume of data that they did, using less transmitting power. They used a concatenation of Reed-Solomon code and convolutional code.

Many early applications of coding were developed for National Aeronautics and Space Administration (NASA) and European Space Agency (ESA) deep Space and satellite communication systems where power was very expensive and bandwidth was plentiful.
A deep Space mission is expensive and additional cost for developing and implementing complex error correcting codes (ECC) encoder and decoder is required, which can be tolerated. Each decibel of coding gain realised resulted in an overall saving of about one million dollars (in 1960’s) in transmitting and receiving equipment. Because of this, mathematician Massey referred to deep Space communication and coding as a marriage made in heaven.

When Voyager sent pictures of Jupiter’s moons in 1979, it was 640 million kilometres from Earth. A year later, it sent clear close-up shots of Saturn’s rings. In 1986, when transmitting near Uranus, Voyager was about three billion kilometres away. And in 1989, after being 12 years on the road to the outer reaches of the solar system, and nearly five billion kilometres away from Earth, it was able to transmit incredibly-detailed, perfectly-focused pictures of Triton, Neptune’s largest moon.
Storage media. error correcting codes (ECCs) are extensively used in storage systems. BCH codes and Reed-Solomon codes are used in applications like compact disk players, DVDs, disk drives, NAND flash drives and 2D bar codes. LDPC codes are considered as the choice of error correcting codes (ECC) for SSDs and fountain codes are erasure codes used in data-storage applications.
A typical audio CD can hold up to 70 minutes of music. In fact, it takes about 1.5 million bits to represent just one second of music. These bits are represented by pits on the mirror-like surface on one side of the disk. The pits have an average length of about one micron, and are recorded along a spiral track, which is about 0.5 microns wide. Here, scratches, dust and fingerprints cause errors that are eliminated by using ECC.
Mobile communication. We know different generations of mobile communication, namely, 1G, 2G, 3G, 4G and 5G, which give us improved data rate with improved data-handling capabilities. This is made possible by sophisticated communication systems where error control coding is integral.
ARQ is sometimes used with Global System for Mobile (GSM) communication to guarantee data integrity. Traffic channels generally in 2G standard use convolution code. Convolution and turbo codes are used in 3G (UMTS) networks; convolution coding can be used for low data rates and turbo coding for higher rates.
WiMAX (IEEE 802.16e standard for microwave communications) and high-speed wireless LAN (IEEE 802.11n) use LDPC as a coding scheme.
Satellite communication. Applications of error control techniques enhance reliability of the down-link of telemetry parameters such as satellite down-link state and of photographic image data of a CCD camera, ensuring reliable data transmission of the chain between satellites, the chain between Earth and satellites and lowering error rate.
For long-distance telephony, digital cinema, digital video broadcasting (DVB-S2/DVB-T2/DVBC2), navigation and remote monitoring for secure and reliable data transmission error control coding is the solution. LDPC codes are now used in many high-speed communication standards, such as DVB-S2.
Current scenario and scope
As the demand for Big Data processing (retrieving at receiver or reproduction from storage) with high speed, consuming less power and utilising bandwidth efficiently grows, adaptive error control coding along with adaptive modulation is the solution. So coding with stronger ability of error correction is used when the state of channel is poor and coding with higher utilisation rate is used when the state of channel is better.

For reliable communication in WiMax, optical communication and power line communication, or in multi-layer flash memories, implementation of advanced forward ECC scheme should be considered, like turbo and LDPC codes.
Hybrid ARQ is another technique for spectrum efficiency and reliable link. Network coding is one of the most important breakthroughs in information theory in recent years.
A variety of codes are available, one for every different application. To learn coding theory, sound knowledge of Algebra (Group, Ring, Field, Galois theory), probability and information theory is required.
Do you like this article? You may also like other tech focus articles.
Atul M. Kulkarni is M.Tech in communication engineering from National Institute of Technology (NIT), Karnataka. Currently, he is lecturer at Dr Babasaheb Ambedkar Technological University, Maharashtra. This article has been written under the guidance of Dr Prashantha Kumar H., assistant professor at NIT, Karnataka







Thanks for the article.
You are welcome.