Along with the immense promise of quantum computing come the enhanced security threats too. This has opened up a whole new field known as post quantum security.
“Not only is the Universe stranger than we think, it is stranger than we can think,” opined Werner Heisenberg in his famous book ‘Across the Frontiers.’ This quote aptly applies to a quantum computer, which has amazed computer enthusiasts about its promise and ability to solve the otherwise non-solvable, hard problems in our classical computing world.

Quantum computer promises to speed up every individual instruction processing, thus defying Moore’s Law. But it also promises to quickly solve the exponentially repetitive tasks, such as finding out two prime factors of a given big integer number, which makes it an impending threat for our known cybersecurity universe—a threat to computer’s hardware, software, and stored information. It is a potential threat to our existing cybersecurity concepts and techniques. In this article we shall review this threat to gain a deeper comprehension, so that we can build an opinion around that independently.
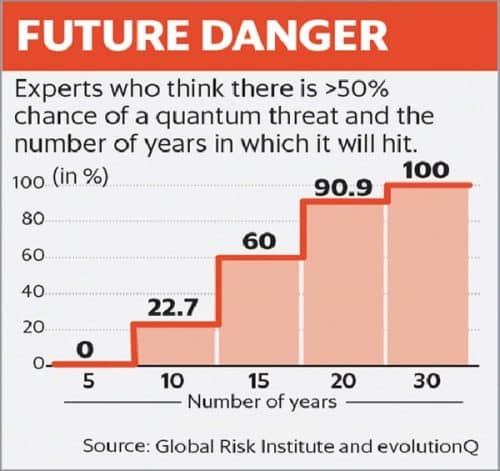
Fig. 1 and Fig. 2 indicate the potential of the so-called quantum threat and the global investment behind it; seemingly China is leading the pack.

Existing cybersecurity techniques
One obvious method of cracking an encryption code is by brute force; keep trying all possible combinations till the code is broken. But this brute force method is not very practical as it may take years to try out all the combinations of a key. So, the current state of affairs depends on public key encryption. Some well-known techniques are: Diffie-Hellman, elliptic curve, and RSA.
Let us look at RSA. It is related to getting the private key by continuously factoring the public key, a big integer, into product of two primes. Till now this is non-trackable in classical computer paradigm. Because it starts with a big enough integer, it takes years to get the private key out, when compromised. Roughly, the key generation algorithm can be stated as below:
- Get two equal-size random prime numbers, say p and q.
- Make sure the product of p and q (let’s call it n) is of desired bit length, say 1024.
- Let’s compute the value of n and Ǿ= (p-1) (q-1)
- Let’s select a proper integer e between 1 and Ǿ
- Secret component derivation: d, again between 1 and Ǿ,→ed=1 mod Ǿ
- The public key part is (n, e) and private part is (d, p, q).
- d, p, q and Ǿ are secrets.
Quantum cybersecurity perspective
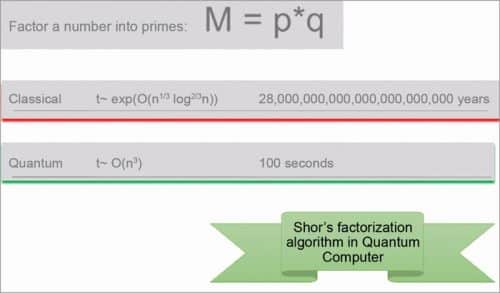
The prime factorisation we discussed above, when tried out in classical computer, takes a very long time to be computed. This makes it practically invincible, so we feel secure that our classical security model is intact and in place. However, that is not the case for quantum computing paradigm. Fig. 3 describes a mind-blowing comparison of prime factorisation across classical and quantum computing paradigms. The corresponding quantum computing prime factorisation algorithm is known as Shor’s Algorithm.
The above figure vividly depicts the potential risks of proliferation of quantum computing in the cybersecurity paradigm. To understand the contour of cybersecurity in the quantum age we need to first define what is quantum safe security? Quantum safe security is often called post quantum security as well. Like any modelling of a security problem, let us start with the worst.
Let us say the honest party has only the classical computer and the adversary is quantum powered. Let us assume the adversary’s quantum power does not necessarily exist today, it can be futuristic also—to make the problem statement interesting. In the classical world we would like to build a security mechanism that cannot be compromised, even by the quantum powered adversary. Winning in such unfavorable condition is called post quantum security. This is one area attracting intense research interest today.
Let us look at the remediation—how to achieve such a post quantum security paradigm.
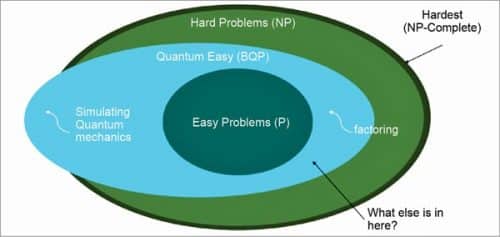
To understand this seemingly unbelievable world of post quantum security we need to understand what sort of problems a quantum computer can potentially solve. Can it solve any NP complete (hardest) problem? No, it cannot. Fig. 4 depicts the Bounder Error Polynomial (BQP) time, which is the problem zone quantum computers can solve in polynomial time.
As we can see in Fig. 4, there still exists an unsolvable zone which is quantum-hard also. It means this zone is out of reach for classical as well as quantum computers. Now, intuitively, if we can devise our security primitives and constructs in that zone (the green colour zone in Fig. 4), then we are safe. Well, we are right, but partially. Having security primitives in the green zone in Fig. 4 is necessary, but not sufficient to prove the quantum safety of the solution.
There are believed to be some security techniques available today which are promising in post quantum order, such as secret-key cryptography. However, the quantum property of the quantum computer, on the other hand, raises additional security attack surface as well. One such example is Superposition Attack. Stating in simple terms, superposition is a quantum property where a qubit (a bit in quantum computer is called qubit) can posses 0, 1, or a mix of 0 and 1 values. Once you measure the qubit, it collapses to either classical 0 or classical 1. Now an adversary, powered by the quantum computer oracle, can potentially learn the superposition ciphertexts of some plain text and decipher the superposition using another algorithm (without directly measuring the superposition ciphertext) to acquire knowledge about the cryptosystem. That’s it.
One can, of course, argue that to pose such a threat to our contemporary, classical security primitives, one needs to have a big enough (of many qubit) fault-tolerant and stable quantum computer—which will be happening in near future but not happening tomorrow. Then why should I right now bother about it? The primary reason is, an adversary can potentially steal our today’s encrypted messages and can decipher them tomorrow, being powered by quantum oracle. And this sort of development requires a holistic research approach and an overhaul of the cryptographic infrastructure, which are time consuming. So better to start today.
Quantum gadgets
Is the picture only so gloomy? Not really. There is silver lining also. We now have something called Quantum Gadget, which can be used to enhance the security of the classical communication primitives. One such example is Quantum Key Distribution (QKD). The idea of QKD is derived from the fact that two honest parties can have a shared random secret key that is only known to them. If any adversary wants to intercept the secret random key, the adversary must read the key. Once a quantum state is read (measured), it collapses to one of the classical states—either 0 or 1. Hence any such adversary intrusion results in a detectable anomaly in the overall system.
There are other ways also a quantum gadget can pave way into our classical security systems and primitives, such as quantum fingerprints. One can think of it as a technique involving a quantum computer to generate a string like our classical cryptographic hash functions. There are various other examples also, but not limited to, like quantum random number generation, quantum signature generation, Byzantine agreement, quantum flip-the-coin, secure e-voting, secure multi-party computation, etc.
In nutshell
Quantum computer research, as shown in Fig. 2, is widespread and across nations. One of the areas of immediate interest of these researchers is related to making classical devices, communication, and information to be adaptable and secure in post quantum era. Basically, making them quantum safe.
In this article we started off with discussing how our classical notion of security evolves around RSA. Then we discussed the notion and concept around quantum safety. We discussed the necessary but not sufficient condition of keeping our security primitives outside the reach of quantum solvable BQP domain (Fig. 4). At last, we concluded with an optimism that quantum gadgets like quantum key distribution (QKD) are there to help us in near future to achieve quantum safely.
Of course, the journey has just begun, and it is far from concluded with some definitive answers.
This article was first published in April 2020 issue of Open Source For You
Pradip Mukhopadhyay has 19 years of experience across the stack—from low level systems programming to high level GUIs. He is a FOSS enthusiast, and currently works at NetApp, Bengaluru






