Encoding the information before transmission is necessary to ensure data security and efficient delivery of the information. The MATLAB program presented here encodes and decodes the information and also outputs the values of entropy, efficiency and frequency probabilities of characters present in the data stream.

Huffman algorithm is a popular encoding method used in electronics communication systems. It is widely used in all the mainstream compression formats that you might encounter—from GZIP, PKZIP (winzip, etc) and BZIP2, to image formats such as JPEG and PNG. Some programs use just the Huffman coding method, while others use it as one step in a multistep compression process.

Huffman coding & deciding algorithm is used in compressing data with variable-length codes. The shortest codes are assigned to the most frequent characters and the longest codes are assigned to infrequent characters.

Huffman coding is an entropy encoding algorithm used for lossless data compression. Entropy is a measure of the unpredictability of an information stream. Maximum entropy occurs when a stream of data has totally unpredictable bits. A perfectly consistent stream of bits (all zeroes or all ones) is totally predictable (has no entropy).

The Huffman coding method is somewhat similar to the Shannon–Fano method. The main difference between the two methods is that Shannon–Fano constructs its codes from top to bottom (and the bits of each codeword are constructed from left to right), while Huffman constructs a code tree from the bottom up and the bits of each codeword are constructed from right to left.

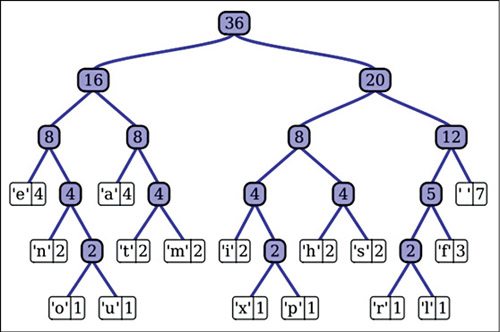
The model for Huffman tree is shown here in the figure. It is generated from the sentence “this is an example of a huffman tree” using Huffman algorithm. Here 36 is the root of the tree. Below the root node you can see the leaf nodes 16 and 20. Adding 16 and 20 gives 36. Adding 8 and 8 gives 16, while 4+4=8. On the left-hand side, ‘e’ is attached to 4. Similarly, ‘a’, ‘n’, ‘t’, etc have been attached to form the complete Huffman tree.

For details on Huffman tree formation, please refer the ‘Data Compression and Decompression’ software project published in EFY April 2005.

The simplest tree construction algorithm uses a priority queue or table where the node with the lowest probability or frequency is given the highest priority.

First, create a leaf node for each symbol or character and add it to the priority table. If there is more than one node in the table, remove two nodes of the highest priority (lowest frequency) from the table. Create a new node with these two nodes as sub-nodes and with probability equal to the sum of the two nodes’ probabilities. Continue in this way until you reach the last single node. The last node is the root, so the tree is now complete.

Steps to encode data using Huffman coding

Step 1. Compute the probability of each character in a set of data.
Step 2. Sort the set of data in ascending order.
Step 3. Create a new node where the left sub-node is the lowest frequency in the sorted list and the right sub-node is the second lowest in the sorted list.
Step 4. Remove these two elements from the sorted list as they are now part of one node and add the probabilities. The result is the probability for the new node.
Step 5. Perform insertion sort on the list.
Step 6. Repeat steps 3, 4 and 5 until you have only one node left.[/stextbox]

Now that there is one node remaining, simply draw the tree.

With the above tree, place a ‘0’ on each path going to the left and a ‘1’ on each path going to the right. Now assign the binary code to each of the symbols or characters by counting 0’s and 1’s starting from the root.

Since efficient priority-queue data structures require O(log n) time per insertion, and a tree with ‘n’ leaves has 2n−1 nodes, this algorithm operates in O(n log n) time, where ‘n’ is the number of symbols.

From the above, it is now clear that the encoding method should give rise to a uniquely decodable code so that the original message can be detected uniquely and perfectly without errors. The message generated with the highest probability will be generated more number of times than other messages. In such a case, if you use a variable-length code instead of a fixed-length code, you will be improving the efficiency by assigning fewer bits to the higher-probability messages than the lower-probability messages.

How MATLAB program works

1. List the source probabilities in decreasing order.

2. Combine the probabilities of the two symbols having the lowest probabilities, and record the resultant probabilities; this step is called reduction.
This procedure is repeated until there are two-order probabilities remaining.

3. Start encoding with the last reduction, which consists of exactly two-order probabilities. Assign ‘0’ as the first digit in the code words for all the source symbols associated with the first probability; assign ‘1’ to the second probability.

4. Now go back and assign ‘0’ and ‘1’ to the second digit for the two probabilities that were combined in the previous reduction step, retaining all assignments made in Step 3.

5. Keep regressing in this way until the first column is reached.

6. Calculate the entropy. The entropy of the code is the average number of bits needed to decode a given pattern.

7. Calculate efficiency. For evaluating the source code generated, you need to calculate its efficiency.

Efficiency = Entropy (H(X))/Average codeword length (N)

Average codeword length is given by:
N =∑(Pi × Ni)
where Ni is the length of ith codeword and Pi is the probability of occurence.

MATLAB functions

Huffmanenco. This function is used in Huffman coding. The syntax is:

comp = huffmanenco(sig,dict)

This line encodes the signal ‘sig’ described by the ‘dict’ dictionary. The argument ‘sig’ can have the form of a numeric vector, numeric cell array or alphanumeric cell array. If ‘sig’ is a cell array, it must be either a row or a column. The ‘dict’ is an Nx2 cell array, where ‘N’ is the number of distinct possible symbols to be encoded. The first column of ‘dict’ represents the distinct symbols and the second column represents the corresponding codewords. Each codeword is represented as a numeric row vector, and no codeword in ‘dict’ can be the prefix of any other codeword in ‘dict’. You can generate ‘dict’ using the huffmandict function.

Huffmandeco. This function is used in Huffman decoding. The syntax is:

dsig = huffmandeco(comp,dict)

This line decodes the numeric Huffman code vector comp using the code dictionary ‘dict’. The argument ‘dict’ is an Nx2 cell array, where ‘N’ is the number of distinct possible symbols in the original signal that was encoded as ‘comp’. The first column of ‘dict’ represents the distinct symbols and the second column represents the corresponding codewords. Each codeword is represented as a numeric row vector, and no codeword in ‘dict’ is allowed to be the prefix of any other codeword in ‘dict’. You can generate ‘dict’ using the Huffmandict function and ‘comp’ using the huffmanenco function. If all signal values in ‘dict’ are numeric, ‘dsig’ is a vector; if any signal value in ‘dict’ is alphabetical, ‘dsig’ is a one-dimensional cell array.

Testing

1. Launch the MATLAB program. The program first generates the dictionary of messages. These messages are nothing but codes or bitstreams from 00 to 1001 in this example. You can extend this range by changing in the source code. The MATLAB program output for the example is given below:

Enter the probabilities: [0.3 0.25
0.2 0.12 0.08 0.05]
The huffman code dict:
[1] ‘0 0’
[2] ‘0 1’
[3] ‘1 1’
[4] ‘1 0 1’
[5] ‘1 0 0 0’
[6] ‘1 0 0 1’
Enter the symbols between 1 to 6
in[]:[3]
sym = 3
The encoded output:
1 1
Enter the bit stream in[];[1 1]
The symbols are: 3
Entropy is 2.360147 bits
Efficiency is 0.991659
m = 4
s = 2
Variance: 2

2. First, the program prompts you to enter the number between ‘1’ and ‘6’. When you enter ‘3’, code ‘1 1’ appears on the screen. This code is nothing but the character corresponding to number ‘3’. Hence encoding is done successfully.

3. For decoding, enter bitstream ‘1 1’. The output generated is ‘3’.

4. Instead of ‘3’, you can try out using various combinations from ‘1’ to ‘6’.

The program outputs the values of maximum length (m) and minimum length (s) generated in the dictionary. The maximum length generated is ‘1111’, i.e., m=4. The minimum length is ‘00’, which is two bits long and therefore s=2.

Huffman coding is also called Minimum-variance coding. Variance is maximum length-minimum length. Hence variance is ‘2’ in this example.

Download Source Code: click here

---

Feel Interested! Check out these MATLAB Projects.